Preface :
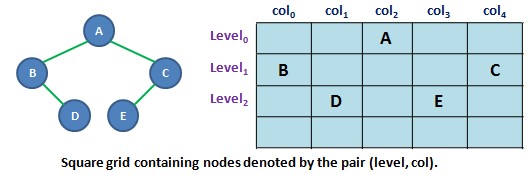
View the display of the tree as a rectangular grid with a cell denoted by the pair (level, column) in console. The level is a row in the grid corresponding to a level in the tree. The column coordinate designates a region of the display measured left to right. Below figure is the representation of Tree in the grid. The algorithm to display a tree uses a recursive scan to create a copy of the original tree. The copy is called a shadow tree. The nodes of the shadow tree store the value of the node in the original tree formatted as a string and the (level, col) position of the shadow tree node in the grid. A level-order scan of the shadow tree displays the nodes :
Building a Shadow Tree :
The recursive function buildShadowTree() uses an inorder scan (LNR) of the original tree to build a shadow tree. As the inorder scan progress, we move from one grid column to another. For instance, with Tree upper, the order of visits is B > D > A > E > C. Note in upper figure that this is the column-order for the nodes in the tree.
A shadow tree uses an augmented node structure for its elements. The TNodeShadow objects have the basic TNode structure, with additional variables leveland column that specify the coordinates for a cell in the grid. The variable nodeValueStr is a string that describe the value for a node in the original tree. For instance, if a tree node has integer 135, then the nodeValueStr in the corresponding shadow tree is "135".
The algorithm for buildShadowTree() resembles copyTree() with the exception that it makes an inorder scan of the original tree rather than a postorder scan. Each recursive call allocates a TNodeShado object and assigns it the string that corresponds to the value of the node in the original tree. If then makes recursive calls that create the left and right subtrees. You will notice that TNodeShadow class has a static variable columnValue. This variable is key to the algorithm. Because the variables is static, it is global to the recursive process. Each recursive call in the inorder scan creates a node in the column specified by columnValue and then increments the variable for the subsequent recursive call. In this way, columnValue has values ranging from 0 for the first visit (left most node) to n-1 for a visit to the rightmost node. The buildShadowTree() method has two parameters. The TNode reference t provides access to the value of the original tree node. An integer denotes the level in the tree :
Displaying a Shadow Tree :
The method displayTree() takes the root t, of the binary tree as an argument and calls buildShadowTree() to create a shadow tree :
// build the shadow tree
TNodeShadow shadowRoot = buildShadowTree(t, 0);
The algorithm displays the tree using a level-order scan of shadow tree nodes. Each shadow tree node provides the node value as a string and the (level, column) coordinate for an element. The scan uses a queue of TNodeShadow objects to store and access the nodes. As shadow tree nodes emerge from the queue the displayTree() method positions the value at (level, col) in the grid. To determine the location of each node in the grid, we use the argumentmaxCharacters, which is the number of characters in the longest node value. The variable colWidth, with value maxCharacters + 1, defines the width of each cell in the display. The variable currLevel is the current level during the scan and variable currCol is the current column coordinate in the grid. The string representation of the tree is stored in the variable displayStr.
As nodes are popped from the queue into the reference variable currNode, display Tree() carries out of the task of displaying the node value (currNode.nodeValueStr) at the grid coordinates (currNode.level, currNode.column). The column position combines with the value of colWidth to specify how far we must move to the right before inserting the node. Because the level-order scan visits siblings from left to right, the distance of the move is determined by comparing the column positions for successive siblings. The variable currLevel maintains a record of the current level (line) on which nodes are displayed. The value of the currLevel is incremented whenever a node is popped from the queue with a level greater than colLevel. The implementation simply inserts a newline character to move down one level. The string continues to add node values on the same level until another change is required. The private methods formatString() output a string in a specified number of print positions. They are used to position the tree nodes in their proper columns. Below is the whole implementation of how to display a tree :
View the display of the tree as a rectangular grid with a cell denoted by the pair (level, column) in console. The level is a row in the grid corresponding to a level in the tree. The column coordinate designates a region of the display measured left to right. Below figure is the representation of Tree in the grid. The algorithm to display a tree uses a recursive scan to create a copy of the original tree. The copy is called a shadow tree. The nodes of the shadow tree store the value of the node in the original tree formatted as a string and the (level, col) position of the shadow tree node in the grid. A level-order scan of the shadow tree displays the nodes :

Building a Shadow Tree :
The recursive function buildShadowTree() uses an inorder scan (LNR) of the original tree to build a shadow tree. As the inorder scan progress, we move from one grid column to another. For instance, with Tree upper, the order of visits is B > D > A > E > C. Note in upper figure that this is the column-order for the nodes in the tree.
A shadow tree uses an augmented node structure for its elements. The TNodeShadow objects have the basic TNode structure, with additional variables leveland column that specify the coordinates for a cell in the grid. The variable nodeValueStr is a string that describe the value for a node in the original tree. For instance, if a tree node has integer 135, then the nodeValueStr in the corresponding shadow tree is "135".
The algorithm for buildShadowTree() resembles copyTree() with the exception that it makes an inorder scan of the original tree rather than a postorder scan. Each recursive call allocates a TNodeShado object and assigns it the string that corresponds to the value of the node in the original tree. If then makes recursive calls that create the left and right subtrees. You will notice that TNodeShadow class has a static variable columnValue. This variable is key to the algorithm. Because the variables is static, it is global to the recursive process. Each recursive call in the inorder scan creates a node in the column specified by columnValue and then increments the variable for the subsequent recursive call. In this way, columnValue has values ranging from 0 for the first visit (left most node) to n-1 for a visit to the rightmost node. The buildShadowTree() method has two parameters. The TNode reference t provides access to the value of the original tree node. An integer denotes the level in the tree :
Displaying a Shadow Tree :
The method displayTree() takes the root t, of the binary tree as an argument and calls buildShadowTree() to create a shadow tree :
// build the shadow tree
TNodeShadow shadowRoot = buildShadowTree(t, 0);
The algorithm displays the tree using a level-order scan of shadow tree nodes. Each shadow tree node provides the node value as a string and the (level, column) coordinate for an element. The scan uses a queue of TNodeShadow objects to store and access the nodes. As shadow tree nodes emerge from the queue the displayTree() method positions the value at (level, col) in the grid. To determine the location of each node in the grid, we use the argumentmaxCharacters, which is the number of characters in the longest node value. The variable colWidth, with value maxCharacters + 1, defines the width of each cell in the display. The variable currLevel is the current level during the scan and variable currCol is the current column coordinate in the grid. The string representation of the tree is stored in the variable displayStr.
As nodes are popped from the queue into the reference variable currNode, display Tree() carries out of the task of displaying the node value (currNode.nodeValueStr) at the grid coordinates (currNode.level, currNode.column). The column position combines with the value of colWidth to specify how far we must move to the right before inserting the node. Because the level-order scan visits siblings from left to right, the distance of the move is determined by comparing the column positions for successive siblings. The variable currLevel maintains a record of the current level (line) on which nodes are displayed. The value of the currLevel is incremented whenever a node is popped from the queue with a level greater than colLevel. The implementation simply inserts a newline character to move down one level. The string continues to add node values on the same level until another change is required. The private methods formatString() output a string in a specified number of print positions. They are used to position the tree nodes in their proper columns. Below is the whole implementation of how to display a tree :
This message was edited 2 times. Last update was at 22/03/2011 09:59:01

沒有留言:
張貼留言