Source From Here
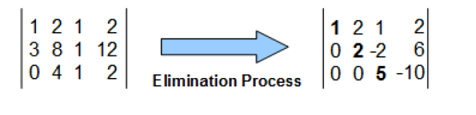
Elimination Process
Consider we have system equations as below:
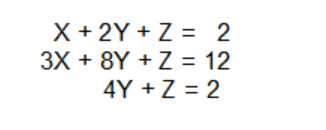
Actually, we can treat it as a matrix multiplication: Ax=b
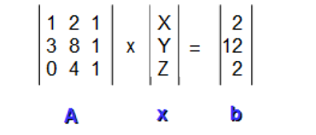
Then we can use Gaussian elimination to help use solve the equations: A=LU
Augmented Matrix
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices. Take upper equation as example:
Then let's change back to our system equations:

Matrix Multiplication
For matrix multiplication, we can use different view point to do the calculation.
Matrix * Column : Column Combination of Matrix
Matrix multiple Column will produce a Column which is the combination of each column of Matrix. For example:
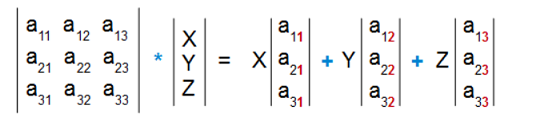
Let's use code to test this concept:
Row * Matrix = Row : Row Combination of Matrix
Row multiple Matrix will produce Row which is the row combination of Matrix (1xN * NxN = 1xN). For example:
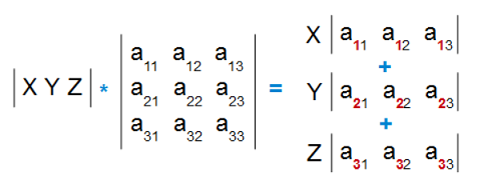
Let's use code to test this concept:
Block Operations
If we divide Matrix into multiple blocks, then we can treat that block as an bigger element and do multiplication with block composition. For example:
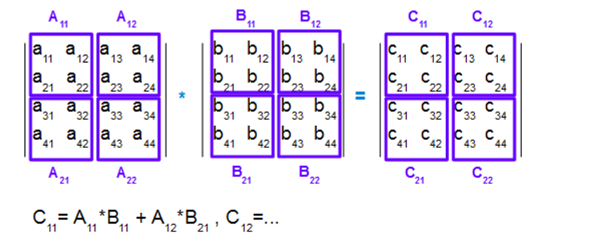
Let's use code to test this concept:
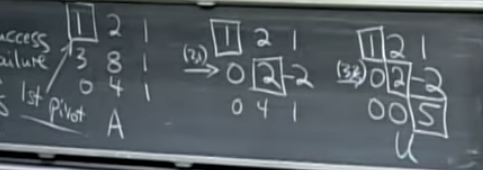
Elimination Matrix
Actually, the elimination process can be presented with a matrix. For example:
The row [-3, 1, 0] of the left matrix can be explained as operation on target matrix: Row1*-3 + Row2
E21 means this elimination matrix is to erase M[2,1] (M is target matrix) to be zero. For next step:
Finally, we get the elimination matrx:
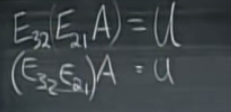
Permutation
Consider we have a matrix like:
How do I switch column 0 with column 1 by matrix multiplication? Remember that we learn from different view of multiplication, the matrix multiplication can be column combination. So let's do it by multiple the matrix with a special matrix:
For the same principle, we can switch row by letting special matrix multiple our target multiple:
Elimination Process
Consider we have system equations as below:
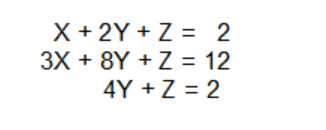
Actually, we can treat it as a matrix multiplication: Ax=b
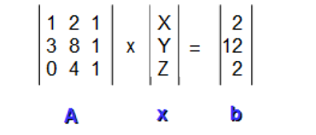
Then we can use Gaussian elimination to help use solve the equations: A=LU

Augmented Matrix
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices. Take upper equation as example:

Then let's change back to our system equations:

Matrix Multiplication
For matrix multiplication, we can use different view point to do the calculation.
Matrix * Column : Column Combination of Matrix
Matrix multiple Column will produce a Column which is the combination of each column of Matrix. For example:
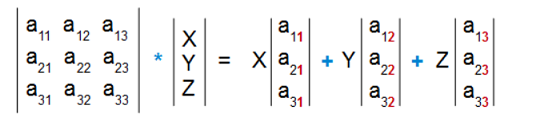
Let's use code to test this concept:
Row * Matrix = Row : Row Combination of Matrix
Row multiple Matrix will produce Row which is the row combination of Matrix (1xN * NxN = 1xN). For example:
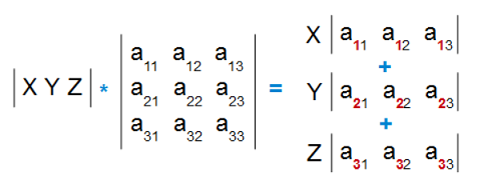
Let's use code to test this concept:
Block Operations
If we divide Matrix into multiple blocks, then we can treat that block as an bigger element and do multiplication with block composition. For example:

Let's use code to test this concept:
Elimination Matrix
Actually, the elimination process can be presented with a matrix. For example:
The row [-3, 1, 0] of the left matrix can be explained as operation on target matrix: Row1*-3 + Row2
E21 means this elimination matrix is to erase M[2,1] (M is target matrix) to be zero. For next step:
Finally, we get the elimination matrx:
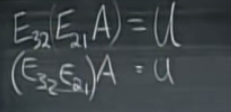
Permutation
Consider we have a matrix like:
How do I switch column 0 with column 1 by matrix multiplication? Remember that we learn from different view of multiplication, the matrix multiplication can be column combination. So let's do it by multiple the matrix with a special matrix:
For the same principle, we can switch row by letting special matrix multiple our target multiple:




沒有留言:
張貼留言