[ 資料結構 小學堂 ] 圖形結構 : 圖形的追蹤

前言 : 
樹的追蹤目的是欲拜訪樹的每一節點一次, 可用的方法有中序, 前序與後序等三種. 而圖形追蹤定義如下 : 

一圖形 G=(V,E), 存在某一頂點 v, 我們希望從v 開始並經由此節點的相鄰節點而去拜訪G 中其他節點, 這稱之為圖形追蹤.

也就是從某一頂點V1 開始, 走訪可以經由V1 到達的頂點, 接著再走訪下一個頂點直到全部的頂點走訪完畢為止. 在走訪的過程中可能會重複過某些頂點及邊線. 經由圖形的走訪可以判斷圖形是否連通, 並找出連通單元及路徑. 圖形走訪的方法有兩種 : "先深後廣走訪" 及 "先廣後深走訪". 

先深後廣法 : 
先深後廣走訪的方式有點類似前序走訪. 是從圖形的某一頂點開始走訪, 被拜訪過的頂點就作上已拜訪的記號, 接著走訪此頂點的所有相鄰且未拜訪過的頂點中的任意一個頂點, 並做上已拜訪的記號, 再以該點為新的起點繼續進行先深後廣的搜尋. 
這種圖形追蹤方法結合了遞迴與堆疊兩種資料結構的技巧, 由於不小心會造成無窮迴路, 所以必須加上一個變數, 判斷該節點是否已經走訪完畢. 
底下我們以下圖來看看這個方法的走訪過程 : 
 
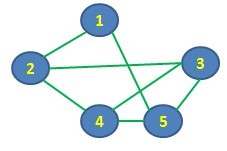
步驟一 : 以頂點1 為起點, 將相鄰的頂點2及頂點5放入堆疊. (頂點1已拜訪) 
 
步驟二 : 取出頂點2, 將頂點2相鄰且未拜訪過的頂點3及頂點4放入堆疊. (頂點1,2 已拜訪) 
 
步驟三 : 取出頂點3, 將與頂點3相鄰且未拜訪過的頂點4 及頂點5放進堆疊. (頂點1,2,3 已拜訪) 
 
步驟四 : 取出頂點4, 將與頂點4相鄰且未拜訪過的頂點5放入堆疊. (頂點1,2,3,4 已拜訪) 
 
步驟五 : 取出頂點5, 將與頂點5相鄰且未拜訪過的頂點放入堆疊, 這裡與頂點5相鄰的頂點已經都拜訪過, 所以無須再放入堆疊. (頂點1,2,3,4,5 已拜訪) 
 
步驟六 : 將堆疊內的值取出並判斷是否已經走訪過, 直到堆疊內無節點可走訪為止. 故先深後廣的走訪順序為 : 頂點1, 頂點2, 頂點3, 頂點4, 頂點5. 

範例代碼 : 

view plaincopy to clipboardprint?

1. #include   
2.   
3. using namespace std;  
4.   
5. class graphicPoint{  
6. public:  
7.     int val;  
8.     class graphicPoint *next;  
9.     graphicPoint(){  
10.         next = NULL;  
11.         val = -1;  
12.     }  
13. };  
14.   
15. int run[6] = {0};  
16. class graphicPoint head[6]; // 共有5個頂點  
17. void dfs(int current) {  
18.     graphicPoint *ptr;  
19.     run[current] = 1;  
20.     cout << "[" << current << "] ";  
21.     ptr = head[current].next;  
22.     while(ptr!=NULL) {  
23.         if(run[ptr->val]==0)  
24.             dfs(ptr->val);  
25.         ptr = ptr->next;  
26.     }  
27. }  
28. void main(bool b) {  
29.     if(b) {       
30.         int data[14][2] = {{1,2}, {2,1}, {1,5}, {5,1}, {2,3}, {3,2}, {2,4}, {4,2}, {3,4}, {4,3}, {3,5}, {5,3}, {4,5}, {5,4}}; //圖形邊線陣列宣告  
31.         for(int i=0; i<14; i++) {  
32.             int tmpi = data[i][0];  
33.             int tmpj = data[i][1];  
34.             graphicPoint *npt = new graphicPoint;  
35.             npt->val = tmpj;  
36.             graphicPoint *pt = &head[tmpi];  
37.             while(pt->next != NULL)  
38.                 pt = pt->next;  
39.             pt->next = npt;            
40.         }  
41.         cout << "圖形鄰接串列內容 : " << endl;  
42.         for(int i=1; i<6; i++) {  
43.             graphicPoint *pt = head[i].next;  
44.             cout << "頂點 " << i << "=>";  
45.             while(pt!=NULL)  {  
46.                 cout << "[" << pt->val << "] ";  
47.                 pt  = pt->next;  
48.             }  
49.             cout << endl;  
50.         }  
51.         cout << "深度優先走訪頂點 :" << endl;  
52.         for(int i=0; i<6; i++) { // 初始化run 陣列  
53.             run[i] = 0;  
54.         }  
55.         dfs(1);  // 以頂點1為起點  
56.         printf("\n");  
57.     }  
58. }  

執行結果 : 

圖形鄰接串列內容 :
頂點 1=>[2] [5]
頂點 2=>[1] [3] [4]
頂點 3=>[2] [4] [5]
頂點 4=>[2] [3] [5]
頂點 5=>[1] [3] [4]
深度優先走訪頂點 :
[1] [2] [3] [4] [5]

補充說明 : 
* [ 資料結構 小學堂 ] 圖形結構 : 圖形表示法